¡Hasta Aquí llegamos con el tema Triángulos espero volverlos a ver para las próximas Unidades!

Profesor: Ríos, Julio Ricardo

Clase Nº 4

TEOREMA DE PITÁGORAS

Hace años, un hombre llamado Pitágoras descubrió un hecho asombroso sobre triángulos:

Si el triángulo tiene un ángulo recto (90°)...

... y pones un cuadrado sobre cada uno de sus lados, entonces...

... ¡el cuadrado más grande tiene exactamente la misma área que los otros dos cuadrados juntos!

El lado más largo del triángulo se llama "hipotenusa", así que la definición formal es: 

En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)

Entonces, el cuadrado de a (a²) más el cuadrado de b (b²) es igual al cuadrado de c (c²):

a² + b² = c²

¿Seguro... ?

Veamos si funciona con un ejemplo. Un triángulo de lados "3,4,5" tiene un ángulo recto, así que la fórmula debería funcionar.

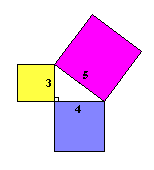Veamos si las áreas son la misma: 32 + 42 = 52 Calculando obtenemos: 9 + 16 = 25 ¡sí, funciona!

Ahora veremos una demostración sencilla para que quede claro el tema

¿Por qué es útil esto?

Si sabemos las longitudes de dos lados de un triángulo con un ángulo recto, el Teorema de Pitágoras nos ayuda a encontrar la longitud del tercer lado. (¡Pero recuerda que sólo funciona en triángulos rectángulos!)

¿Cómo lo uso?

Escríbelo como una ecuación:

a2 + b2 = c2

Ahora puedes usar álgebra para encontrar el valor que falta, como en estos ejemplos:

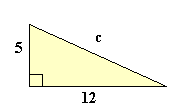
a2 + b2 = c2 52 + 122 = c2 25 + 144 = 169 c2 = 169 c = √169 c = 13

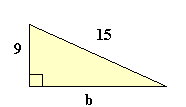
a2 + b2 = c2 92 + b2 = 152 81 + b2 = 225 Resta 81 a ambos lados b2 = 144 b = √144 b = 12

Nota histórica: aunque se llama Teorema de Pitágoras, ¡también lo conocían los matemáticos indios, griegos, chinos y babilonios antes de que él viviera!

REPASO DE LA CLASE ANTERIOR

Clasificación de triángulos.

Aquí les dejo un material para que puedan comprender mejor el tema.

Actividades de Repaso  >>>>>> Actividad Nº3

Clase Nº 3

Chicos hoy comenzaremos la clase con clasificación de los triángulos según sus ángulos.

CLASIFICACIÓN DE LOS TRIÁNGULOS SEGÚN SUS ÁNGULOS

Se dividen en:

1) Triángulos acutángulos: Tienen TRES ángulos agudos (menores de 90º).

En el dibujo siguiente tienes dos triángulos acutángulos.

2) Triángulos obtusángulos: Tienen UN ángulo obtuso (más de 90º).

En la siguiente figura tienes dos triángulos obtusángulos

3) Triángulos rectángulos: Tienen UN ángulo recto.

Tienes a continuación tres ejemplos de triángulos rectángulos

En un triángulo rectángulo, el lado opuesto al ángulo recto se llama hipotenusa y los lados perpendiculares que forman el ángulo recto se llaman catetos.

Actividad a realizar  >>>>>> Actividad Nº2

CLASE Nº 2

TRIÁNGULOS:

DEFINICIÓN Y CLASIFICACIÓN

 Triángulo: Es todo polígono cerrado de tres lados. Todo Triángulo tiene tres vértices, tres ángulos interiores y tres ángulos exteriores.

Ahora entrarán a los siguiente enlaces donde podrán leer

 “La historia de Isósceles el Triángulo” 

Historia "1era Parte"

Historia "2da Parte"

CLASIFICACIÓN DE LOS TRIÁNGULOS SEGÚN SUS LADOS

Los nombres que reciben son:

1) Triángulos Equiláteros

Las palabras equi - látero vienen del latín: igual – lado.

Son los triángulos cuyos tres lados son iguales: (a=b=c)

2) Triángulos Isósceles
La palabra isósceles está compuesta de dos palabras griegas iso que significa igual y de la palabra skeles que podemos traducir por piernas.

La palabra isósceles referido a la geometría quiere decir que dos lados (piernas) son iguales. Por lo tanto, un triángulo con dos lados iguales llamamos isósceles.

Como ves en la figura, tienes el triángulo isósceles con dos lados iguales. Si tiene 2 lados iguales tendrá también dos ángulos iguales.

3) Triángulos Escalenos

La palabra escaleno procede de la palabra griega skaleno que significa cojear, cojo. Nos da la idea que si el triángulo “cojea” sus lados no son iguales. Efectivamente, el triángulo escaleno tiene sus lados diferentes por lo que sus ángulos también serán diferentes.

Aquí les propongo una actividad que traerán resuelta para la siguiente clase ---->>>> Actividad Nº1

CLASE Nº 1

Para comenzar con esta clase veremos el siguiente vídeo, en el cual aprenderemos cuales son los elementos de un triángulo.

ENTRAR AQUÍ...............>>>>>>   Elementos de un triángulo

Podrán ver una ficha ilustrativa donde queda plasmados los elementos del Triángulo, que luego pegarán en sus carpetas

        

 ·        Construirán  una definición de triángulo a partir de las siguientes palabras claves que verán a continuación.

 ·        Traerán para la próxima clase las definiciones que han podido elaborar.

Bienvenidos Chicos a nuestro primer contacto en este blog, aquí aprenderemos la Unidad de Triángulos, con esto se pretende que aprendan un poco mas sobre el tema.

Aquí le dejo el mapa conceptual referido a lo que aprenderemos en el transcurso de esta Unidad

Me gustaría que dejen comentarios sobre lo que piensan o creen,  que es un triángulo

Estos comentarios serán leídos en clases así conoceré lo que piensan.

"No se puede enseñar nada a un hombre; sólo se le puede ayudar a encontrar la respuesta dentro de sí mismo."


Galileo Galilei